Understanding Back Propagation Neural Network Architectures

Once you understand Feed Forward mechanism which isn't much useful when you do not back propagate to update the weights and refine your Neural Network, your Neural Network isn't of much use. So in this blog post, let us understand what is back propagation and how could we represent the back propagation mathematically!

Back propagation generally means that you distribute the errors to the hidden layers in a proportionate manner relative to how much the weights were contributing to the actual error in the subsequent layer. so the larger the weight, the more of the output error is carried back to the hidden layer.

As always, here is a sheet of paper where I have worked out the Math (Matrix representation). I have vectorised the back propagation mechanism!

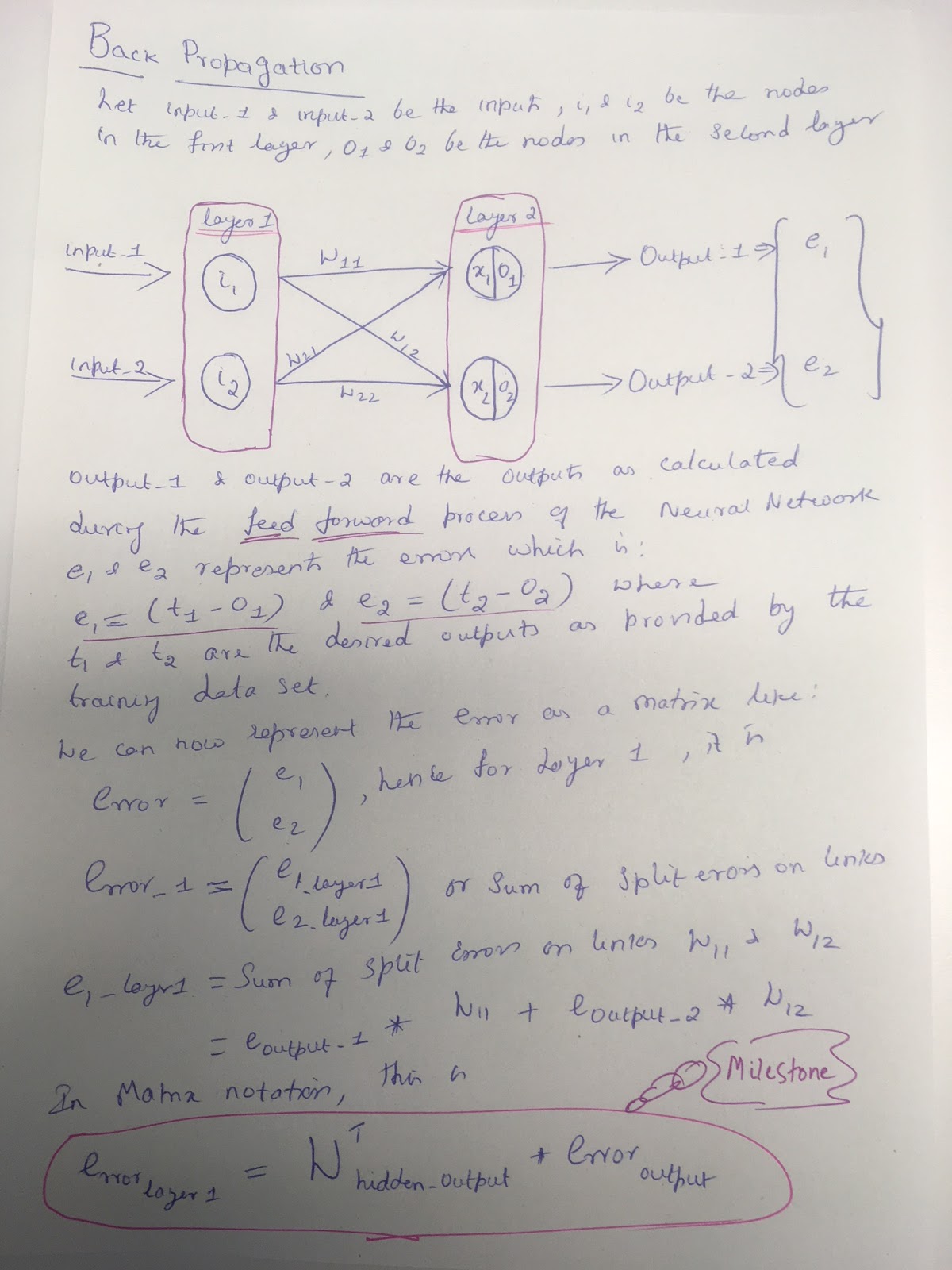
Now you might wonder from where did I arrive at my Milestone matrix notation. If you expand on that W^T_{hidden_output} you will find out that this weights matrix is just a Transpose of the original weights Matrix during the forward propagation phase. This is a big step in understanding the way we distribute the errors into the subsequent hidden layers of the Neural Networks.

The hidden_output in my sheet above in the simple 2 layer, 2 node network mean that my hidden layer is also the input layer. The reason why I decided to call it as hidden_output is for the fact that a typical Neural Network will not just have an input and an output layer, but also several hidden layers. So don't be confused with the hidden_output, well I could have as well called it input_output! But nevertheless, you get the message! Don't you?